GAMES101作业本——作业6：加速结构

作业描述

在之前的编程练习中实现了基础的光线追踪算法，具体而言是光线传输、光线与三角形求交。采用了这样的方法寻找光线与场景的交点：遍历场景中的所有物体，判断光线是否与它相交。在场景中的物体数量不大时，该做法可以取得良好的结果，但当物体数量增多、模型变得更加复杂，该做法将会变得非常低效。因此，需要加速结构来加速求交过程。在本次练习中，重点关注物体划分算法 Bounding Volume Hierarchy (BVH)。本练习要求实现 Ray-Bounding Volume 求交与 BVH 查找。

首先，需要从上一次编程练习中引用以下函数：

Render() in Renderer.cpp: 将光线生成过程粘贴到此处，并且按照新框架更新相应调用的格式。
Triangle::getIntersection in Triangle.hpp: 将光线-三角形相交函数粘贴到此处，并且按照新框架更新相应相交信息的格式。

在本次编程练习中，需要实现以下函数：

IntersectP(const Ray& ray, const Vector3f& invDir, const std::array& dirIsNeg) in the Bounds3.hpp: 这个函数的作用是判断包围盒 BoundingBox 与光线是否相交，需要按照课程介绍的算法实现求交过程。
getIntersection(BVHBuildNode node, const Ray ray)* in BVH.cpp: 建立 BVH 之后，我们可以用它加速求交过程。该过程递归进行，将在其中调用你实现的 Bounds3::IntersectP.

附加题：

SAH 查找：自学 SAH(Surface Area Heuristic) , 正确实现 SAH 加速，并对比 BVH、SVH 的时间开销。(可参考 http://15462.courses.cs.cmu.edu/fall2015/lecture/acceleration/slide_024，也可以查找其他资料)

解题思路

1 修改Render()函数

作业框架发生了一些改变，根据数据类型的变化做一些相应的调整。eyepos 的位置在(-1, 5, 10)，屏幕的中心坐标就不在 (0,0,-1)了，而是位于 (-1,5,9)。但射线方向其实与作业5求法相同。

Vector3f dir = normalize(Vector3f(x, y, -1));
Ray ray = Ray(eye_pos, dir);
framebuffer[m++] = scene.castRay(ray, 0);

2 修改Triangle::getIntersection

上一次作业中函数判断光线是否与三角形相交并返回一个布尔值。此次作业中需要返回相交的信息。

inline Intersection Triangle::getIntersection(Ray ray)
{
    Intersection inter;

    // 点积大于零，两向量夹角小于90度，此时与光线和三角形不可能相交
    if (dotProduct(ray.direction, normal) > 0)
        return inter;
    double u, v, t_tmp = 0;
    Vector3f pvec = crossProduct(ray.direction, e2);
    double det = dotProduct(e1, pvec);
    if (fabs(det) < EPSILON)
        return inter;

    double det_inv = 1. / det;
    Vector3f tvec = ray.origin - v0;
    u = dotProduct(tvec, pvec) * det_inv;
    if (u < 0 || u > 1)
        return inter;
    Vector3f qvec = crossProduct(tvec, e1);
    v = dotProduct(ray.direction, qvec) * det_inv;
    if (v < 0 || u + v > 1)
        return inter;
    t_tmp = dotProduct(e2, qvec) * det_inv;

    // DONE: find ray triangle intersection
    if (t_tmp < 0)
        return inter;
    inter.happened = true; // 是否相交
    inter.coords = ray(t_tmp); // 交点坐标
    inter.normal = normal; // 交点所在平面法线
    inter.distance = t_tmp; // 光线出射时间
    inter.obj = this; // 交点所在物体的物体类型
    inter.m = m; // 三角形的材质

    return inter;
}

3 实现IntersectP函数

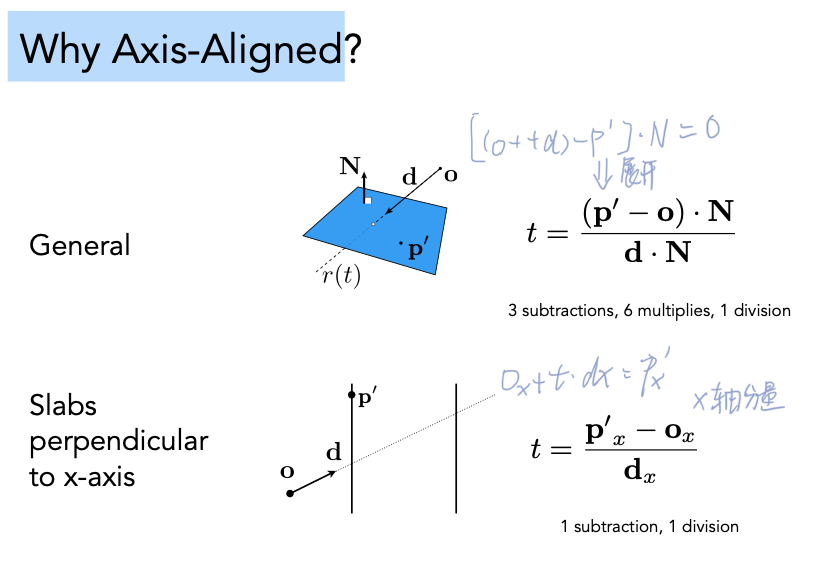
这个函数的作用是判断包围盒 BoundingBox 与光线是否相交。

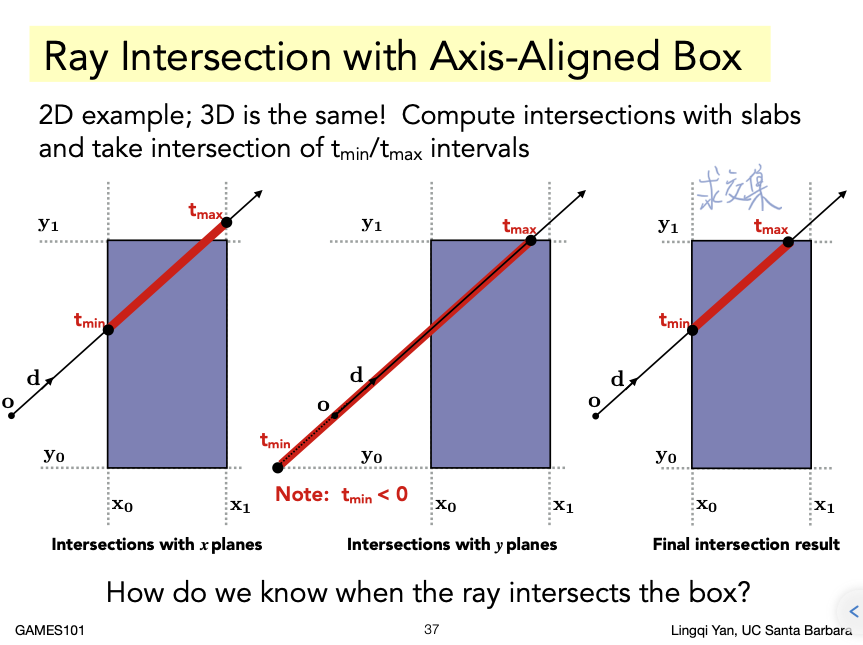
观察给出的Bounds3类，可知三维包围盒上是用两个点：三轴坐标最小点pMin和三轴坐标最大点pMax来表示，此时两个点刚好在包围盒的六个面上。结合射线的方程很容易能解出与每个面的交点。

class Bounds3
{
  public:
    Vector3f pMin, pMax; // two points to specify the bounding box
    Bounds3()
    {
        double minNum = std::numeric_limits<double>::lowest();
        double maxNum = std::numeric_limits<double>::max();
        pMax = Vector3f(minNum, minNum, minNum);
        pMin = Vector3f(maxNum, maxNum, maxNum);
    }
    Bounds3(const Vector3f p) : pMin(p), pMax(p) {}
    Bounds3(const Vector3f p1, const Vector3f p2)
    {
        pMin = Vector3f(fmin(p1.x, p2.x), fmin(p1.y, p2.y), fmin(p1.z, p2.z));
        pMax = Vector3f(fmax(p1.x, p2.x), fmax(p1.y, p2.y), fmax(p1.z, p2.z));
    }

inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
    const std::array<int, 3>& dirIsNeg) const {
    // invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z), use this because Multiply is faster that Division
    // dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)], use this to simplify your logic
    // Done: test if ray bound intersects
    // 化简了一下运算，没有使用dirIsNeg，实际上和每条轴分别运算并判断方向的解法一样

    Vector3f tMin = Vector3f::Min((pMin - ray.origin) * invDir, (pMax - ray.origin) * invDir);
    Vector3f tMax = Vector3f::Max((pMin - ray.origin) * invDir, (pMax - ray.origin) * invDir);

    float tEnter = std::max(tMin.x, std::max(tMin.y, tMin.z));
    float tExit = std::min(tMax.x, std::min(tMax.y, tMax.z));

    return (tEnter < tExit) && (tExit >= 0);
}

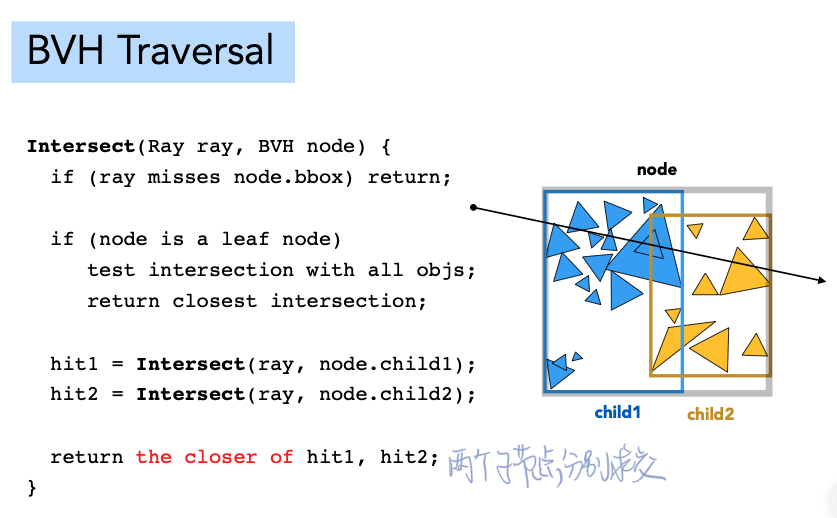
4 实现getIntersection

递归遍历二叉树。

Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const {
    // DONE: Traverse the BVH to find intersection
    Intersection isect;

    // 没有交点
    if (node == nullptr || !node->bounds.IntersectP(ray, ray.direction_inv, { 0,0,0 }))
        return isect;

    // 有交点且为叶子结点
    if (node->left == nullptr && node->right == nullptr)
        // 调用obj子类：Triangle的getIntersection，即到叶子节点的包围盒开始与三角形求交
        return node->object->getIntersection(ray);

    Intersection hit1 = getIntersection(node->left, ray);
    Intersection hit2 = getIntersection(node->right, ray);

    return hit1.distance < hit2.distance ? hit1 : hit2;
}

BVH Generation complete: 
Time Taken: 0 hrs, 0 mins, 0 secs

 - Generating BVH...

BVH Generation complete: 
Time Taken: 0 hrs, 0 mins, 0 secs

Render complete: ======================================================] 100 %
Time taken: 0 hours
          : 0 minutes
          : 6 seconds

使用BVH加速算法渲染作业模型耗时6秒。

附加：SAH查找

BVH加速通常是选取三角形中位数位置分割子树，这种划分方式可以再优化。

这里构建了一个评估函数计算节点的开销，优化的目标是划分空间时使这个式子的值最小。

对于每个轴，将其等距离划分成B份，得到B-1个划分平面。对于第i个平面，把三角形的中点集合划分成两份，计算这两份的开销，选取开销最小的平面。

计算三个轴，选开销最小的轴。

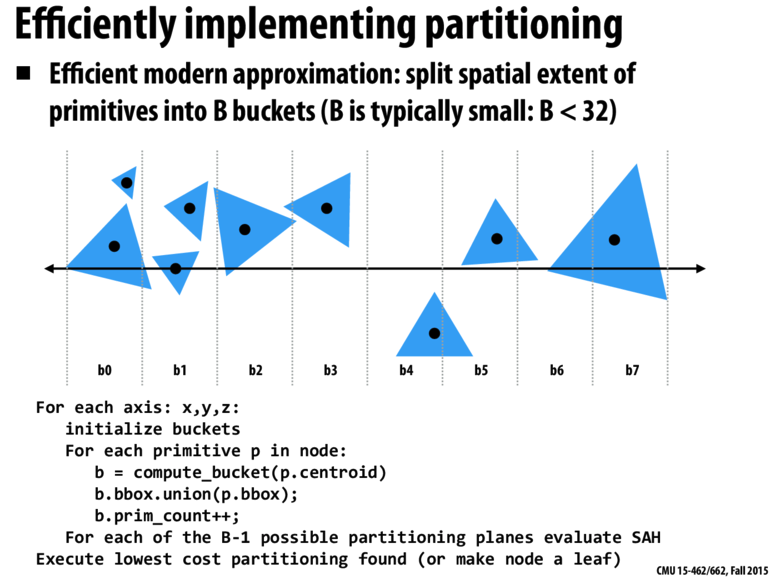
可能是Stanford Bunny模型的面数太少，使用SAH加速后渲染时间与BVH无异，换了另一个面数更高的小牛的模型时间也还是一样。主要实现代码如下：

BVHAccel::BVHAccel(std::vector<Object*> p, int maxPrimsInNode,
    SplitMethod splitMethod)
    : maxPrimsInNode(std::min(255, maxPrimsInNode)), splitMethod(splitMethod),
    primitives(std::move(p)) {
    time_t start, stop;
    time(&start);
    if (primitives.empty())
        return;

    if (splitMethod == SplitMethod::NAIVE) {
        root = root = recursiveBuild(primitives);
    }
    else if (splitMethod == SplitMethod::SAH) {
        root = root = recursiveSAHBuild(primitives);
    }


    time(&stop);
    double diff = difftime(stop, start);
    int hrs = (int)diff / 3600;
    int mins = ((int)diff / 60) - (hrs * 60);
    int secs = (int)diff - (hrs * 3600) - (mins * 60);

    printf(
        "\rBVH Generation complete: \nTime Taken: %i hrs, %i mins, %i secs\n\n",
        hrs, mins, secs);
}

BVHBuildNode* BVHAccel::recursiveSAHBuild(std::vector<Object*> objects) {
    BVHBuildNode* node = new BVHBuildNode();

    // Compute bounds of all primitives in BVH node
    Bounds3 bounds;
    for (int i = 0; i < objects.size(); ++i)
        bounds = Union(bounds, objects[i]->getBounds());
    // 剩下一个，直接设为叶子结点
    if (objects.size() == 1) {
        // Create leaf _BVHBuildNode_
        node->bounds = objects[0]->getBounds();
        node->object = objects[0];
        node->left = nullptr;
        node->right = nullptr;
        return node;
    }
    // 剩下两个，左子树一个右子树一个
    else if (objects.size() == 2) {
        node->left = recursiveBuild(std::vector{ objects[0] });
        node->right = recursiveBuild(std::vector{ objects[1] });

        node->bounds = Union(node->left->bounds, node->right->bounds);
        return node;
    }
    else {
        Bounds3 centroidBounds;
        // 求整体包围盒
        for (int i = 0; i < objects.size(); ++i)
            centroidBounds =
            Union(centroidBounds, objects[i]->getBounds().Centroid());
        // SAH相关参数
        float Sn = centroidBounds.SurfaceArea();
        int B = 10; // B is typically small than 32
        int minCostCoor = 0; // 最优分割轴
        int minCostIndex = 0; // 最优分割区块值
        float minCost = std::numeric_limits<float>::infinity(); // 最小开销

        // 分别计算三个轴
        for (int i = 0; i < 3; ++i) {
            switch (i) {
                case 0:
                    // 对x排序
                    std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {return f1->getBounds().Centroid().x < f2->getBounds().Centroid().x;});
                    break;
                case 1:
                    // 对y排序
                    std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {return f1->getBounds().Centroid().y < f2->getBounds().Centroid().y;});
                    break;
                case 2:
                    // 对z排序
                    std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {return f1->getBounds().Centroid().z < f2->getBounds().Centroid().z;});
                    break;
                default:
                    break;
            }
            for (int j = 1; j < B; ++j) {
                auto beginning = objects.begin();
                auto middling = objects.begin() + (objects.size() * j / B);
                auto ending = objects.end();
                auto leftShapes = std::vector<Object*>(beginning, middling);
                auto rightShapes = std::vector<Object*>(middling, ending);

                Bounds3 leftBounds, rightBounds;
                for (int k = 0; k < leftShapes.size(); ++k)
                    leftBounds =
                    Union(leftBounds, leftShapes[k]->getBounds().Centroid());
                for (int k = 0; k < rightShapes.size(); ++k)
                    rightBounds =
                    Union(rightBounds, rightShapes[k]->getBounds().Centroid());
                float SA = leftBounds.SurfaceArea();
                float SB = rightBounds.SurfaceArea();
                float cost = 1 + (leftShapes.size() * SA + rightShapes.size() * SB) / Sn;
                if (cost < minCost) {
                    minCost = cost;
                    minCostIndex = j;
                    minCostCoor = i;
                }
            }
        }

        switch (minCostCoor) {
            case 0:
                // x轴最长，对x排序
                std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {return f1->getBounds().Centroid().x < f2->getBounds().Centroid().x;});
                break;
            case 1:
                // y轴最长，对y排序
                std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {return f1->getBounds().Centroid().y < f2->getBounds().Centroid().y;});
                break;
            case 2:
                // z轴最长，对z排序
                std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {return f1->getBounds().Centroid().z < f2->getBounds().Centroid().z;});
                break;
            default:
                break;
        }

        auto beginning = objects.begin();
        auto middling = objects.begin() + (objects.size() * minCostIndex / B);
        auto ending = objects.end();
        auto leftShapes = std::vector<Object*>(beginning, middling);
        auto rightShapes = std::vector<Object*>(middling, ending);
        assert(objects.size() == (leftShapes.size() + rightShapes.size()));
        node->left = recursiveSAHBuild(leftShapes);
        node->right = recursiveSAHBuild(rightShapes);
        node->bounds = Union(node->left->bounds, node->right->bounds);
    }
    return node;
}