作业描述
在光线追踪中最重要的操作之一就是找到光线与物体的交点。一旦找到光线与物体的交点,就可以执行着色并返回像素颜色。在这次作业中,需要实现两个部分:光线的生成和光线与三角的相交。
本次代码框架的工作流程为:
- 从 main 函数开始。定义场景的参数,添加物体(球体或三角形)到场景中,并设置其材质,然后将光源添加到场景中。
- 调用 Render(scene) 函数。在遍历所有像素的循环里,生成对应的光线并将返回的颜色保存在帧缓冲区(framebuffer)中。在渲染过程结束后,帧缓冲区中的信息将被保存为图像。
- 在生成像素对应的光线后,调用 CastRay 函数,该函数调用 trace 来查询光线与场景中最近的对象的交点。
- 然后,在此交点执行着色。此处设置了三种不同的着色情况,并且框架已经提供了代码。
需要修改的函数是:
- Renderer.cpp 中的 Render():这里需要为每个像素生成一条对应的光线,然后调用函数 castRay() 来得到颜色,最后将颜色存储在帧缓冲区的相应像素中。
- Triangle.hpp 中的 rayTriangleIntersect(): v0, v1, v2 是三角形的三个顶点,orig 是光线的起点,dir 是光线单位化的方向向量。tnear, u, v 是需要使用课上推导的 Moller-Trumbore 算法来更新的参数。
解题思路
首先要实现一条从摄像机出发的光线(primar ray),根据此文Ray-Tracing: Generating Camera Rays和作业框架可以得到以下推理过程:
-
按照惯例,平面通常放置在距离相机原点1个单位的位置,且相机看向-Z轴。
-
代码框架中的i、j是raster space下的x、y坐标(以左上角为原点),需要对它们+0.5得到像素中心。为了使之参与计算,需要转换成world space。具体流程如下:
-
将raster space下的像素坐标压缩至[0, 1],转换为NDC space(Normalized Device Coordinates)。
$$ { PixelNDC }_{x}=\frac{\left( { Pixel }_{x}+0.5\right)}{ { ImageWidth }} $$$$ { PixelNDC }_{y}=\frac{\left( { Pixel }_{y}+0.5\right)}{ { ImageHeight }} $$ -
将得到的坐标变换成screen space下的坐标(范围是[-1, 1],此处y轴需要反向)。
$$ { PixelScreen }_{x}=2 * { PixelNDC }_{x}-1 $$$$ { PixelScreen }_{y}=1 - 2 * { PixelNDC }_{y} $$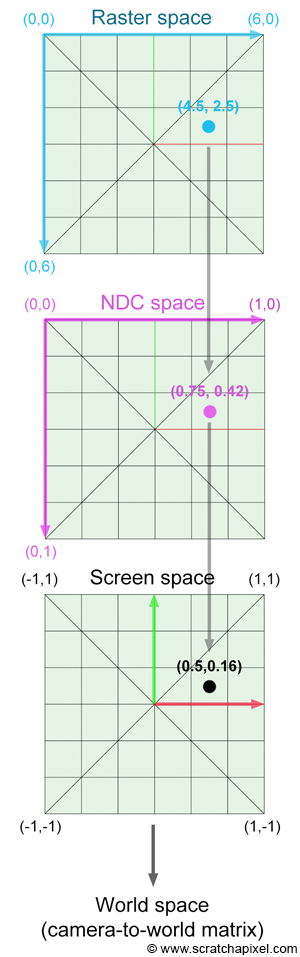
-
为了保持像素比例,需要计算出屏幕宽高比并变换。
$$ { ImageAspectRatio }=\frac{ { ImageWidth }}{ { ImageHeight }} {, } \\ $$$$ { PixelCamera }_{x}=\left(2 * { PixelScreen }_{x}-1\right) *{ ImageAspectRatio, }\\ $$$$ { PixelCamera }_{y}=\left(1-2* { PixelScreen }_{y}\right) {. } \\ $$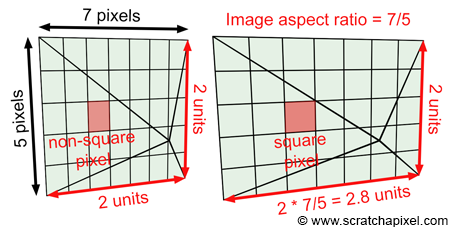
-
为了得出camera space下的坐标需要加上视角信息。从作业框架中得知AB长度为1,那么缩放scale等于BC的长度,易得:
$$ \| B C\|=\tan \left(\frac{\alpha}{2}\right) \\ $$$$ { PixelCamera }_{x}=\left(2 * { PixelScreen }_{x}-1\right) *{ ImageAspectRatio }* { tan }\left(\frac{\alpha}{2}\right) \\ $$$$ { PixelCamera }_{y}=\left(1-2 * { PixelScreen }_{y}\right) * \tan \left(\frac{\alpha}{2}\right) \\ $$$$ P_{ {cameraspace }}=\left( { PixelCamera }_{x}, { PixelCamera }_{y},-1\right) $$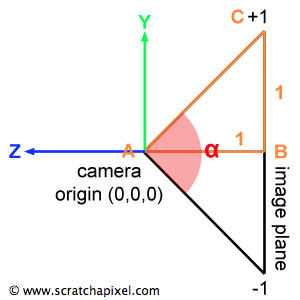
-
因为作业里的相机在坐标系原点,经过以上步骤便可以得出射线。若将相机移动到其他地方,则需要使用camera-to-world matrix计算出变换后的射线。
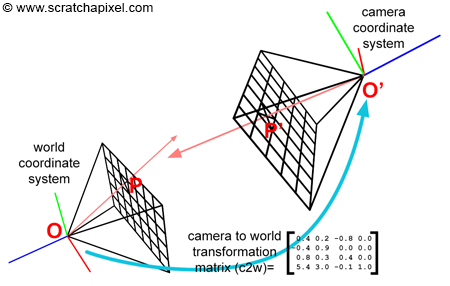
-
接着要将射线与三角形求交,使用课上推导的Möller–Trumbore 算法即可。注意代码框架中tnear、u、v分别对应t、b1、b2。

代码实现
// [comment]
// The main render function. This where we iterate over all pixels in the image, generate
// primary rays and cast these rays into the scene. The content of the framebuffer is
// saved to a file.
// [/comment]
void Renderer::Render(const Scene& scene) {
std::vector<Vector3f> framebuffer(scene.width * scene.height);
float scale = std::tan(deg2rad(scene.fov * 0.5f));
float imageAspectRatio = scene.width / (float)scene.height;
// Use this variable as the eye position to start your rays.
// 摄像机位置在原点,看向-z方向
Vector3f eye_pos(0);
int m = 0;
for (int j = 0; j < scene.height; ++j) {
for (int i = 0; i < scene.width; ++i) {
// generate primary ray direction
float x;
float y;
// DONE: Find the x and y positions of the current pixel to get the direction
// vector that passes through it.
// Also, don't forget to multiply both of them with the variable *scale*, and
// x (horizontal) variable with the *imageAspectRatio*
x = (2 * ((i + 0.5) / scene.width) - 1) * imageAspectRatio * scale;
y = (1 - 2 * ((j + 0.5) / scene.height)) * scale;
Vector3f dir = Vector3f(x, y, -1); // Don't forget to normalize this direction!
dir = normalize(dir);
framebuffer[m++] = castRay(eye_pos, dir, scene, 0);
}
UpdateProgress(j / (float)scene.height);
}
// save framebuffer to file
FILE* fp = fopen("binary.ppm", "wb");
(void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
for (auto i = 0; i < scene.height * scene.width; ++i) {
static unsigned char color[3];
color[0] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].x));
color[1] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].y));
color[2] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].z));
fwrite(color, 1, 3, fp);
}
fclose(fp);
}
bool rayTriangleIntersect(const Vector3f& v0, const Vector3f& v1, const Vector3f& v2, const Vector3f& orig,
const Vector3f& dir, float& tnear, float& u, float& v) {
// DONE: Implement this function that tests whether the triangle
// that's specified bt v0, v1 and v2 intersects with the ray (whose
// origin is *orig* and direction is *dir*)
// Also don't forget to update tnear, u and v.
Vector3f E1 = v1 - v0;
Vector3f E2 = v2 - v0;
Vector3f S = orig - v0;
Vector3f S1 = crossProduct(dir, E2);
Vector3f S2 = crossProduct(S, E1);
float S1_dot_E1 = dotProduct(S1, E1);
float t = dotProduct(S2, E2) / S1_dot_E1;
float b1 = dotProduct(S1, S) / S1_dot_E1;
float b2 = dotProduct(S2, dir) / S1_dot_E1;
float eps = -0.00001; // 避免精度问题造成地板对角线蓝点
if (t >= 0.0 && b1 >= eps && b2 >= eps && (1 - b1 - b2) >= eps) {
tnear = t;
u = b1;
v = b2;
return true;
}
return false;
}
渲染效果:

