GAMES101作业本——作业4：Bézier 曲线

作业描述

Bézier 曲线是一种用于计算机图形学的参数曲线。在本次作业中，需要实现 de Casteljau 算法来绘制由 4 个控制点表示的 Bézier 曲线 (当正确实现该算法时，可以支持绘制由更多点来控制的 Bézier 曲线)。需要修改的函数在提供的 main.cpp 文件中。

bezier：该函数实现绘制 Bézier 曲线的功能。它使用一个控制点序列和一个 OpenCV：：Mat 对象作为输入，没有返回值。它会使 t 在 0 到 1 的范围内进行迭代，并在每次迭代中使 t 增加一个微小值。对于每个需要计算的 t，将调用另一个函数 recursive_bezier，然后该函数将返回在 Bézier 曲线上 t 处的点。最后，将返回的点绘制在 OpenCV ：：Mat 对象上。
recursive_bezier：该函数使用一个控制点序列和一个浮点数 t 作为输入，实现 de Casteljau 算法来返回 Bézier 曲线上对应点的坐标。
附加题：实现对 Bézier 曲线的反走样。(对于一个曲线上的点，不只把它对应于一个像素，你需要根据到像素中心的距离来考虑与它相邻的像素的颜色。)

De Casteljau 算法说明如下：

考虑一个 p0, p1, … pn 为控制点序列的 Bézier 曲线。首先，将相邻的点连接起来以形成线段。
用 t : (1 − t) 的比例细分每个线段，并找到该分割点。
得到的分割点作为新的控制点序列，新序列的长度会减少一。
如果序列只包含一个点，则返回该点并终止。否则，使用新的控制点序列并转到步骤 1。使用 [0,1] 中的多个不同的 t 来执行上述算法，就能得到相应的 Bézier 曲线。

解题思路

解法一：递归

按照作业描述递归实现。

cv::Point2f recursive_bezier(const std::vector<cv::Point2f>& control_points, float t) {
    // DONE: Implement de Casteljau's algorithm

    if (control_points.size() == 1) {
        return control_points[0];
    }
    else {
        std::vector<cv::Point2f> new_control_points;
        for (int i = 1; i < control_points.size(); ++i) {
            new_control_points.emplace_back( control_points[i-1]* (1 - t) + control_points[i] * t);
        }
        return recursive_bezier(new_control_points, t);
    }

}

void bezier(const std::vector<cv::Point2f>& control_points, cv::Mat& window) {
    // DONE: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
    // recursive Bezier algorithm.

    for (double t = 0.0; t <= 1.0; t += 0.001) {
        auto point = recursive_bezier(control_points, t);
        window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
    }

}

解法二：代入递推关系式

代数展开式

int C(int n, int m) {
    int res = 1;
    for (int i = 1; i <= m; ++i) {
        res = res * (n - m + i) / i;
    }
    return res;
}

cv::Point2f recursive_bezier(const std::vector<cv::Point2f>& control_points, float t) {
    // DONE: Implement de Casteljau's algorithm

    auto point = cv::Point2f(0, 0);
    int n = control_points.size() - 1;
    int i = 0;

    for (auto p : control_points) {
        point += p * C(n, i) * std::pow(t, i) * std::pow(1 - t, n - i);
        i++;
    }
    return cv::Point2f(point.x, point.y);

}

void bezier(const std::vector<cv::Point2f>& control_points, cv::Mat& window) {
    // DONE: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
    // recursive Bezier algorithm.

    for (double t = 0.0; t <= 1.0; t += 0.001) {
        auto point = recursive_bezier(control_points, t);
        window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
    }

}

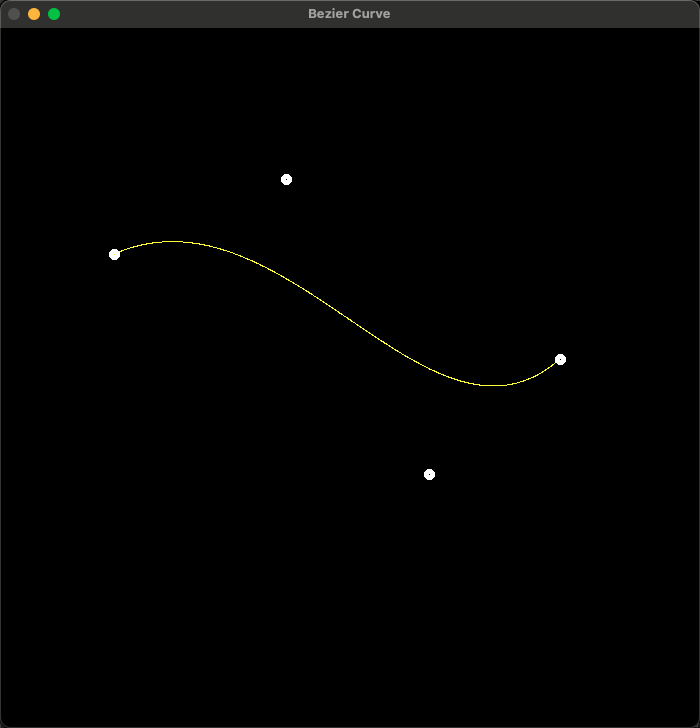
渲染效果

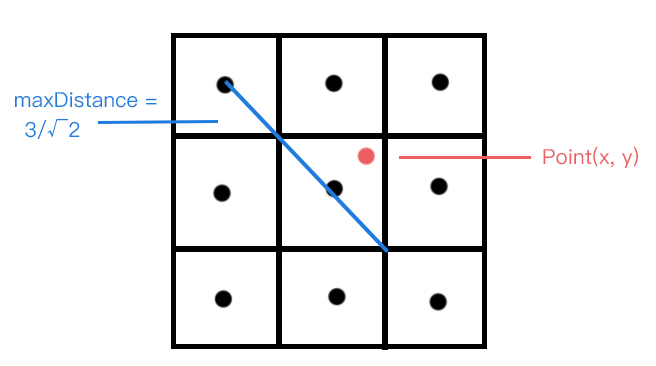
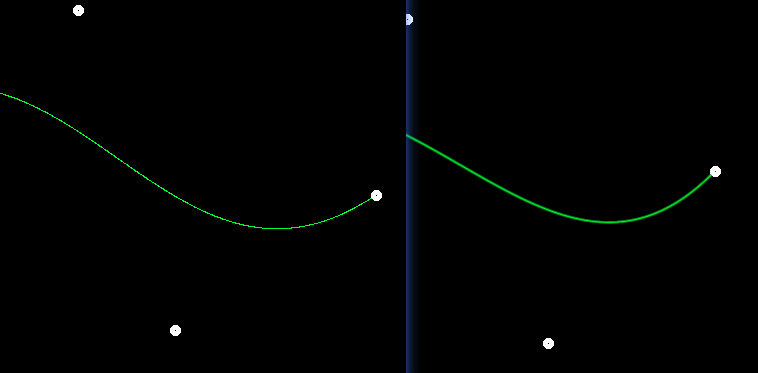
附加题：反走样

对于曲线上的每一个点，计算它到周围3x3个像素中心的距离d，计算与最大距离的比例，用之设置着色浓度。

3x3反走样

效果对比

void bezier(const std::vector<cv::Point2f>& control_points, cv::Mat& window) {
    // DONE: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
    // recursive Bezier algorithm.

    bool anti_aliasing = true;

    for (double t = 0.0; t <= 1.0; t += 0.001) {
        auto point = recursive_bezier(control_points, t);
        if (anti_aliasing) {
            for (float i = -1; i <= 1; i++) {
                for (float j = -1; j <= 1; j++) {
                    // 邻像素点与point间的距离占最大距离（3/√2）之比
                    double ratio = 1 - std::sqrt(2) *
                        std::sqrt(
                            std::pow(point.y - std::floor(point.y + j) - 0.5, 2) + std::pow(point.x - std::floor(point.x + i) - 0.5, 2)) / 3;

                    // 重复的点按照该点的颜色最大值渲染
                    window.at<cv::Vec3b>(std::floor(point.y + j), std::floor(point.x + i))[1] = std::fmax(255 * ratio, window.at<cv::Vec3b>(std::floor(point.y + j), std::floor(point.x + i))[1]);
                }
            }
        }
        else {
            window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
        }
    }

}