作业描述
填写一个旋转矩阵和一个透视投影矩阵。给定三维下三个点 v0(2.0, 0.0, −2.0), v1(0.0, 2.0, −2.0), v2(−2.0, 0.0, −2.0), 你需要将这三个点的坐标变换为屏幕坐标，并在屏幕上绘制出对应的线框三角形 。
理解rasterizer.hpp，修改 main.cpp 中的函数：
- get_model_matrix(float rotation_angle): 逐个元素地构建模型变换矩阵并返回该矩阵。在此函数中，只需要实现三维中绕 z 轴旋转的变换矩阵， 而不用处理平移与缩放。
- get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar): 使用给定的参数逐个元素地构建透视投影矩阵并返回该矩阵。
- [Optional] main(): 自行补充所需的其他操作。
附加题：
- 默认使用 A 和 D 键将该三角形绕 z 轴旋转，实现将三角形绕任意过原点的轴旋转。
解题思路
-
修改get_model_matrix(float rotation_angle)，题目只需要实现三维中绕 z 轴旋转的变换矩阵，矩阵如下： $$ R_z =\begin{pmatrix}cos\alpha &-sin\alpha &0 &0 \\sin\alpha &cos\alpha &0 &0 \\0 &0 &1 &0 \\0 &0 &0 &1 \\\end{pmatrix} $$
-
修改get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)，先做透视变换，再做正交变换，就能得到透视投影所需要的矩阵了。
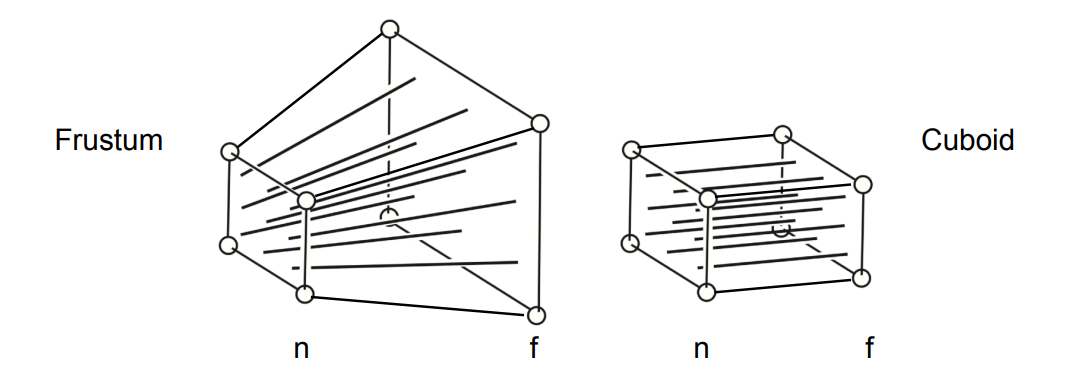
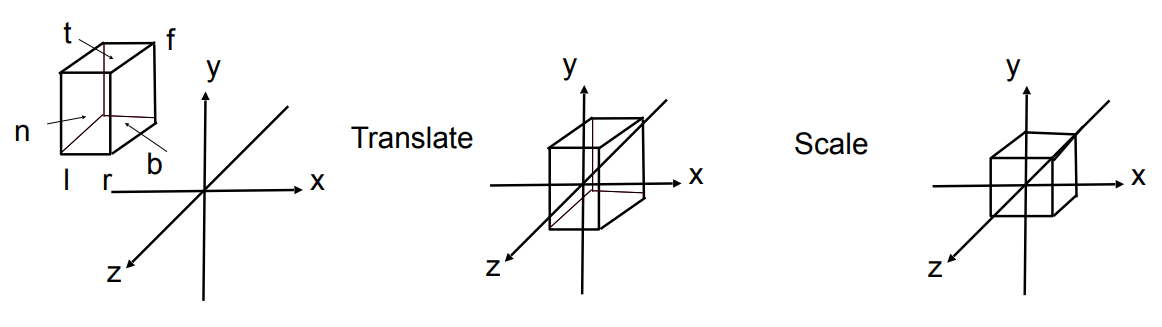
$$ \displaylines{M_{persp\rightarrow ortho} = \begin{pmatrix}n &0 &0 &0 \\0 &n &0 &0 \\0 &0 &n+f &-nf \\0 &0 &1 &0 \\\end{pmatrix}\\\\M_{orth} = \begin{bmatrix} \frac{2}{r-l} &0 &0 &0 \\ 0 &\frac{2}{t-b} &0 &0 \\ 0 &0 &\frac{2}{n-f} &0 \\ 0 &0 &0 &1\end{bmatrix}\begin{bmatrix} 1 &0 &0 &-\frac{r+l}{2} \\ 0 &1 &0 &-\frac{t+b}{2} \\ 0 &0 &1 &-\frac{n+f}{2} \\ 0 &0 &0 &1\end{bmatrix}= \begin{pmatrix}\frac{2}{r-l} &0 &0 &-\frac{r+l}{r-l} \\ 0 &\frac{2}{t-b} &0 &-\frac{t+b}{t-b} \\ 0 &0 &\frac{2}{n-f} &-\frac{n+f}{n-f} \\ 0 &0 &0 &1\end{pmatrix}\\\\M_{persp} = M_{ortho}M_{persp\rightarrow ortho}} $$
题目没有直接给出l、r、b、t，但是提供了Field of view（fov）和Aspect ratio，可以利用它们求出l、r、b、t。
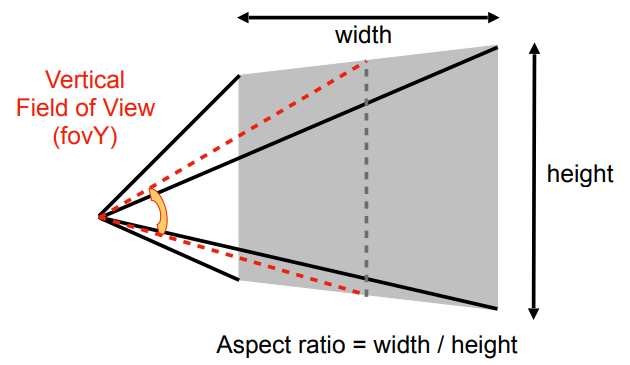
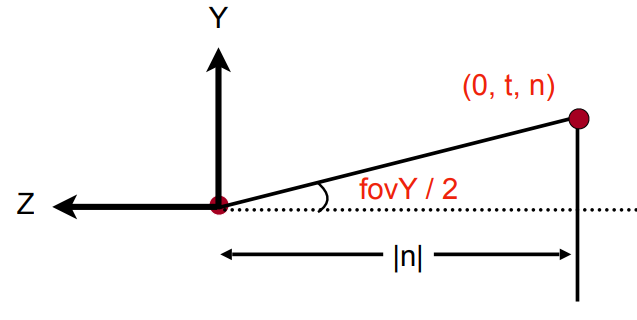$$
\displaylines{\tan\frac{fovY}{2} = \frac{t}{|n|} \\aspect\_ratio = \frac{width}{height} = \frac{2r}{2t} = \frac{r}{t} \\联立得：\\t = |n|\tan\frac{fovY}{2} \\r = aspect\_ratio * t \\b = -t \\l = -r}
$$ -
提高：实现将三角形绕任意过原点的轴旋转需要使用罗德里格旋转公式（Rodrigues’ rotation formula）, 设绕轴n旋转角度α:
$$ \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc}0 & -n_{z} & n_{y} \\n_{z} & 0 & -n_{x} \\-n_{y} & n_{x} & 0\end{array}\right)}_{\mathbf{N}} $$
代码实现
Eigen::Matrix4f get_model_matrix(float rotation_angle){
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
// DONE: Implement this function
// Create the model matrix for rotating the triangle around the Z axis.
// Then return it.
Eigen::Matrix4f rotation;
double angle = rotation_angle / 180.0 * MY_PI;
rotation <<
std::cos(angle), -std::sin(angle), 0, 0,
std::sin(angle), std::cos(angle), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
model = rotation * model;
return model;
}
Eigen::Matrix4f get_model_matrix(Vector3f axis, float rotation_angle){
// DONE提高：绕任意轴旋转
double angle = rotation_angle / 180.0 * MY_PI;
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
Eigen::Matrix3f I = Eigen::Matrix3f::Identity();
Eigen::Matrix3f M;
Eigen::Matrix3f N;
N << 0, -axis[2], axis[1],
axis[2], 0, -axis[0],
-axis[1], axis[0], 0;
M = std::cos(angle) * I + (1 - std::cos(angle)) * axis * axis.adjoint() + std::sin(angle) * N;
model <<
M(0, 0), M(0, 1), M(0, 2), 0,
M(1, 0), M(1, 1), M(1, 2), 0,
M(2, 0), M(2, 1), M(2, 2), 0,
0, 0, 0, 1;
return model;
}
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
float zNear, float zFar){
// Students will implement this function
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
// DONE: Implement this function
// Create the projection matrix for the given parameters.
// Then return it.
Eigen::Matrix4f persp_to_ortho;
Eigen::Matrix4f orth;
float n = -zNear; // Z轴反向
float f = -zFar; // Z轴反向
float t = std::tan(eye_fov / 180 * MY_PI / 2) * std::abs(n);
float r = aspect_ratio * t;
float b = -t;
float l = -r;
persp_to_ortho <<
n, 0, 0, 0,
0, n, 0, 0,
0, 0, n + f, -n * f,
0, 0, 1, 0;
orth <<
2 / (r - l), 0, 0, -(r + l) / (r - l),
0, 2 / (t - b), 0, -(t + b) / (t - b),
0, 0, 2 / (n - f), -(n + f) / (n - f),
0, 0, 0, 1;
projection = orth * persp_to_ortho * projection;
return projection;
}
